The Circle of Fifths - where does it come from, where does it go?

[MAT1953]

When I posted a few weeks ago at the time of Part 1 I said it was perhaps ahead of where I was in Grade 3 Theory, and I would come back to it at a later date, so I didn’t expect it to be back quite as soon…

So, what happened was that I got the Tabs App and disappeared down a rabbit hole about transposing songs to different keys.

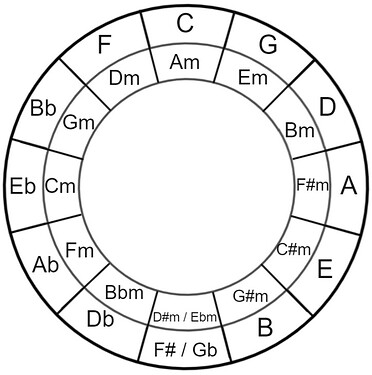
I realised, although I was aware of the following, I didn’t have a clear understanding of how it all fitted together
• Major Scale
• Keys
• Circle of fifths
• Chords in a key and numbering
• Notes in a chord

So, I decided to work my way through the various parts.

Richard @Richard_close2u must say the presentation and way you went through it was excellent. I am the sort of person that if you just gave me the Circle of Fifths and said this is how to use it, I would want to know how it was all put together, which you did. Also liked the way it was developed in stages so you could take in each Part before moving on. Did have to divert occasions to find out things like I didn’t such as what a diatonic chord is.

I appreciate I now only have a very basic and limited overall framework of how things fit together, but I think it will now enable me to fit in the vast number of things I don’t know about that exist, when they come along.

I see that there is now a Part 8 but is there a part that is going to deal with transposing chords into different keys. although I think I do now know how to do it.

Michael

[Richard_close2u]

@MAT1953 Thank you so much for your kind words and appreciation. Knowing that you have gained some musical knowledge and understanding, and enjoyed the experience as you went along, is humbling and heartwarming.
I do have further instalments though I not one explicitly looking at transposing from one key to another. Perhaps I should make a further part looking at that. It follows on simply from some of the implicit comments so far in this overall topic and can be presented readily I would hope.
Cheers.

[MAT1953]

Richard @Richard_close2u

Thanks for the reply.

As I mentioned I got bogged down with transposing because as I am just at the end of Grade 1 guitar and have watched a lot of Justin’s beginner song lessons. In quite a few he says the chords have been ‘changed’ so they are playable with the basic chords you have learned, a lot of them start with the use of a capo to match the original and then get changed. I needed to know what was going on, it is just the way I am.

Obviously there is a danger of introducing too many music theory things at the early stage of the guitar course and if you are interested you get involved in the Theory course, which I did.

As you say having developed the Circle of Fifths this far the ability to transpose is there perhaps a simple explanation of how to do it would be helpful.

Cheers
Michael

[Jeff]

Great stuff Richard. I’m taking this even further by analyzing all of the embellishments and extensions to understand how they fit in the progression.

Most of them sound good because the chord variation uses notes that are found in the key of Bm.

Asus2 = A B E
Asus4 = A D E
Dsus2 = D E A
Dsus4 = D G A
Gsus2 = G A D
F#m7 = F# A C# E
Em7 = E G B D

All good notes there. But then we have this Gsus4, which has the notes G, C and D. In isolation, the note C is probably the worst one to play over a progression B minor.

Yet, it sounds good. Why? My guess would be that we’re borrowing it from the parallel B Phrygian mode?

[Richard_close2u]

The Circle of Fifths Part 8 - where does it go [f] borrowing chords using parallel major & minor keys

Hopefully much useful and plentiful time has been spent exploring and creating diatonic chord progressions in both major keys and minor keys as suggested previously in Part 7.

We have seen major keys. We have seen minor keys – with our focus on the relative minors. We have met and discussed and used the concept of relative major and minor keys in building the inner wheel. Our three examples had, as relative keys; C major and A minor then Ab major and F minor then E major and C# minor.

The entire Circle of Fifths is a quick-glance tool to identify any relative major and minor keys as they are found in corresponding positions on the outer and inner wheels.

[Richard_close2u]

To see how the Circle of Fifths can help us with the concept of borrowing chords we will look at parallel major and minor keys (not relative major and minor).

Note - borrowing chords is also referred to as modal interchange. Under that name, a more expansive concept can be explored. Here, for now, we will be limited to just a small slice of what can be done when chords are ‘borrowed’ from elsewhere.

Parallel major and minor keys are simply one major key and one minor key both of which have the same root note. They do not have the same tonic chord of course, because the tonic of one will be a major chord and the other a minor chord. Hopefully that much is obvious.

Using the three major key examples that have been consistent throughout this study we would have as parallels:

• C major and C minor

• Ab major and Ab minor

• E major and E minor

One major and one minor built from the same root note.

Major in this sense is always THE major scale (Ionian) and minor is always THE minor scale (natural minor or Aeolian) built from the 6th scale degree of its relative major.

So, C major is just the key of C major. Enough said. When we consider its parallel minor key, C minor, we must be aware that it is not the relative minor of C major. Their commonality is the root note. C minor is the relative minor of a different major key – specifically Eb major because C is the 6th scale degree of the Eb major scale.

Look on the outer and inner wheel of the Circle of Fifths above - you will see Eb and Cm in matching positions to confirm this.

That said, there is no need to think that we will be doing all sorts of mathematical equations and counting and trickery to identify what and where the parallel major and minors are. Because we have the Circle of Fifths.

The Circle of Fifths gives us an instant, visual means of finding the parallel keys and their chords. In an instant. No mathematics or tricks involved. We will see that next.

[Richard_close2u]

For ease, we will look just at the C major and C minor parallel keys to begin.

Notice right away that clustered diatonic chords in the key of C major and the clustered diatonic chords in the key of C minor are in directly adjacent positions on the Circle of Fifths. The root note of the Major key is on the outer wheel, the root of the minor key is on the inner wheel.

Remember from earlier, in the key of C major, those six clustered chords represent the diatonic chords I through to vi. Around the outer wheel are the major chords IV, I, V (F, C, G) and around the inner wheel are the minor chords ii, vi, iii (Dm, Am, Em).

We also briefly saw that, viewed from the minor key perspective, the diatonic ordering changes. Looking at the key of C minor we would have on the outer wheel the majors VI, III, VII (Ab, Eb, Bb) and on the inner wheel the minor chords iv, I, v (Fm, Cm, Gm).

Considering the diminished chords for a moment (although we will not be using them), remember how we saw that their root notes sit along the diameter on the opposite side of the circle to the even numbered chords? In the key of C major, the note B (root of B diminished) is directly opposite the ii and IV chords of Dm and F. In the key of C minor, the note D (root of D diminished) is directly opposite the iv and VI chords of Fm and Ab.

We are going to push on in our exploring and begin to operate with two adjacent clusters of six chords from C major and C minor using the concept of borrowing chords. What we now have is an effective doubling of the number of chords available to us in creating chord progressions.

There is a small note of caution. In an introductory, it can be sensible to make sure that the borrowed chords are used sparingly, as little add-ins to complement and take a diatonic to a different sonic space for a brief moment, So the borrowed chord examples we will see will have just a single bar of a borrowed chord surrounded by diatonic chords.

[Richard_close2u]

Example 1

A classic use of a borrowed minor iv chord from the parallel minor key.

The Beatles loved this trick. Subsequently co-opted by a certain Mr Gallagher. It is heard in countless thousands of songs besides.

With a song / chord progression in a major key, the Major IV is played, it then drops to a borrowed minor iv before returning to the tonic.

We have a progression in the key of C major using C and F and a borrowed Fm chord from the key of C minor.

Example 1 - chord progression

Example 1 - audio track

All together … so I start a revolution from my bed …

[Richard_close2u]

Example 2

Another classic.

This time the progression is in the minor key and to create a stronger resolution to finish, the normal minor v chord (Gm) of the minor key is replaced by a borrowed Major V from the parallel major key – played as a dominant G7.

Find any song written in a minor key and the chances are that the dominant is a borrowed V7.

We have a progression in the key of C minor using Cm, Fm, Eb and a borrowed G major chord (played as a G7) from the key of C major.

Example 2 - chord progression

Example 2 - audio track

I couldn’t resist composing this one as a lilting 6/8 dirge. [ Teaser - something happened as a result of this choice involving @brianlarsen … more to come at a later date. ]

[Richard_close2u]

Example 3

Back to playing in a major key and a common chord to borrow is the Major bIII from the parallel minor. This brings an additional major chord option and it can be used in many ways. In this example it links between the IV and the dominant V chord giving a longer lead in to resolve back to the tonic.

We have a progression in the key of C major using C, F, G and a borrowed Eb major chord from the key of C minor.

Example 3 - chord progression

Example 3 - audio track

[Richard_close2u]

Example 4

Once again in the key of C major, we have a progression in which all chords are major but one is out-of-key. Here we have a borrowed bVI from the parallel key of C minor.

We have a progression in the key of C major using C and F and a borrowed Ab major chord from the key of C minor.

Example 4 - chord progression

Example 4 - audio track

[Richard_close2u]

The six main diatonic chords of the parallel major and minor of any given root note / tonic chord will always be found directly adjacent as seen above. The major key chords will always be immediately clockwise from the minor key chords.

This is another of the powerful functions that the Circle of Fifths provides us.

So the task of looking to borrow chords is made simple and easy by simple looking at the Circle of Fifths and finding two adjacent six-chord clusters.

Try to make immediate use of this powerful function by identifying the six major and minor chords belonging to the key of G major and its parallel key of G minor.

Now pick up your guitar and play any chord progression in G major. Any at all. You could perhaps use one of those ten progressions listed in Part 7. But this time do something different. Look next door to the key of Gm minor and grab a chord to borrow and introduce to your progression. You know there’s a reason to learn those barre chords right! All six in the key of Gm require a barre! Yikes.

You did it?
Great!

Did it sound good?
Yes - hooray!
No - play that same chord in a different bar of your progression, or borrow a different chord to see if you like the sound of that one better.

Do the same for the keys D major and D minor.

Do similar for a minor key progression and a borrowed chord from a parallel major key. Perhaps A minor and A major.

Wash, rinse and repeat for any key you like.
Have fun.
Borrow chords and play.

[brianlarsen]

@Richard_close2u

Look next door to the key of Gm minor and grab a chord to borrow and introduce to your progression… All six in the key of Gm require a barre!

Even Dm?

[jjw]

Super interesting.

“Something” by the Beatles uses this. In fact, the chord progression under the main riff is F – Eb – G – C and I always wondered where that Eb came from. Now I know! Thanks.

[Richard_close2u]

@Richard_close2u

All six in the key of Gm require a barre! Yikes.

Whoopsie …

Okay, five of the six.
Eagle eyes Larsen - thanks fella.

[Richard_close2u]

The mystery of the E flat solved at last!

[CD02]

Thanks for this @Richard_close2u so far so good, 100% in the match the pairs test although is feels deep to me

[brianlarsen]

@Richard_close2u

C major → G major

These two major scales overlap and give us the note G on the Circle of Fifths. G is the fifth note in C major (and the root note of G major, our next scale moving clockwiswe).

G major → D major

These two major scales overlap and give us the note D on the Circle of Fifths. D is the fifth note in G major (and the root note of D major, our next scale moving clockwise).

I think these two boxes should be swapped around.
The Miereneurker strikes again

[CD02]

LOL, all this seeming randomness has given me a flashback to the Fibonacci Principle

[Richard_close2u]

@CD02 100% - fab!

@brianlarsen - ooh, good spot on the error (now corrected), thanks.

I love it that you’re both immersing yourselves.