INDEX
Below are links to each of the successive parts as this topic expands.
17 Likes
The Circle of Fifths Part 1 - where does it come from?
I recently added a topic - a journey and exploration into the dark and mysterious world of modes – in which I used the circle of fifths to find modes in parallel.
Writing that topic gave me inspiration to write this new topic devoted to the circle of fifths itself.
What is it?
Where does it come from?
How and why can it be used?
Where does it lead?
We will begin Part 1 with a quite lengthy and, hopefully, a clear and fascinating discovery of a way to consider the origins and creation of the Circle of Fifths. The ‘where does it come from’ part.
ps
Justin’s lessons refer to it as the Cycle of 5ths: The Cycle Of 5ths & The Cycle Of 5ths In Practice
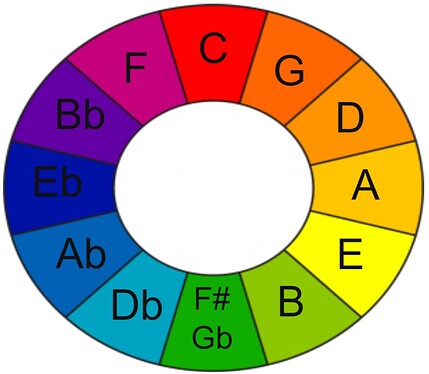
Let us start by taking a look at this glorious tool / work of art / natural phenomenon.
Here it is in beautiful colour (I have overlaid a colour wheel on to the circle).
The Circle of Fifths
There are several points to notice and discuss immediately.
- The letters represent musical notes.
- Like a clock face, there are twelve positions.
- The letter / note C stands at the 12 o’ clock position by convention.
- The letters do not follow in alphabetical order – alphabetical order is not a relevant concept within and around the circle itself.
- Only one pair of enharmonic equivalent notes are shown (F# and Gb at the six o’ clock position). This is my conscious selection. Other enharmonic equivalents do exist and can be used depending on context.
9 Likes
The fundamental approach to creating the Circle of Fifths is to have understanding of the Major Scale, its formula and its structure. The major scale contains seven notes. It is often written with eight where the first note (its root note) is repeated at the end. The intervals between notes are not equal. Rather they follow a strict formula that goes:
Whole – Whole – Half – Whole – Whole – Whole – Half
Whole = one full tone, two semitones, two frets on the guitar.
Half = one semitone, one fret on the guitar.
The formula is also frequently written as:
Tone – Tone – Semitone – Tone – Tone – Tone – Semitone
Both can be abbreviated to:
W – W – H – W - W – W – H and
T – T – S – T – T – T – S respectively.
There is another way of naming these intervals too which assigns each note a syllable. This is called solfege:
Do – Re – Mi – Fa – So – La – Ti – Do
Within this topic the Whole – Half naming convention will be used.
7 Likes
Major Scale Formula over One Octave
This shows the formula and the intervals are represented by the size of the gap between notes.
The notes are numbered 1 to 7 where 1 is the Root note of the scale which is also repeated at the end an octave higher.
Note: the repeated root note is frequently labelled as 8. I have instead chosen to reuse the name 1 for the purpose of showing multiple repeats below.
8 Likes
The fact of the root note appearing twice hopefully creates the easy suggestion that the major scale is not bounded or restricted to just one repeat. It can repeat endlessly. It can be written, seen, and indeed played, as multiple repeats of the same notes, all in sequence, all following the same simple rule given by the major scale formula.
1 – 2 – 3 – 4 – 5 – 6 – 7 – 1 – 2 – 3 – 4 – 5 – 6 – 7 – 1 – 2 – 3 – 4 – 5 – 6 – 7 – 1 …
A grand piano of 88 keys spans over seven octaves altogether.
For any chosen key, those numeric values would be replaced by the appropriate notes of that key’s major scale. For example, the key of A would be:
A - B - C# - D - E - F# - G# - A - B - C# - D - E - F# - G# - A - B - C# - D - E - F# - G# - A …
More useful for our purposes here is the formula describing this repeating major scale.
W – W – H – W – W – W – H - W – W – H – W – W – W – H – W – W – H – W – W – W – H …
This is where the musical and the mathematical can combine – enjoying and exploring the nature of repeating patterns and simple sequences. There is one smaller pattern within the repeated list, one little cluster that recurs throughout this sequence of intervals. A pattern containing just three items.
Can you see it?
Look and look again.
W – W – H – W – W – W – H - W – W – H – W – W – W – H – W – W – H – W – W – W – H …
I am referring to this cluster:
Click to read the hidden answer …
answer
- W – W – H -
Did you identify it?
8 Likes
Here is the same extended sequence with the many repeats of that cluster all shown in bold:
W – W – H – W – W – W – H – W – W – H – W – W – W – H – W – W – H – W – W – W – H …
Viewed like this, not only does that cluster of intervals appear obvious, so too is that each and every cluster is separated by a single ‘W’. The cluster that precedes each stand-alone W is an exact duplicate of the cluster succeeding them.
We are going to modify the diagram above using this newly identified property of the major scale formula to split the eight notes of the scale into two groups of four.
Splitting the Major Scale
The group comprising the first root note, 1, and notes 2, 3 and 4 will be referred to as the lower group.
The group comprising the notes 5, 6 and 7 plus the second root note, 1 will be referred to as the upper group.
Both the lower and upper groups contain four notes defined by the interval cluster:
Whole - Whole - Half (the - W - W - H - identified above).
9 Likes
Moving from the general to the specific, here are some examples of major scales that have been split using this same method.
Split C Major Scale
Split G Major Scale
Split D Major Scale
Take your time to look, really look and make sense of what you see. Look with a keen eye.
11 Likes
Wait a moment.
Take a really close look at the lower and upper groups of C major, G major and D major.
Compare and contrast across all three of the major scales above.
Do you see something amazing?
If not keep looking.

8 Likes
The major scales of C, G and D have not been selected at random.
They have not been selected because they are common keys for chord progressions on guitar.
They have been selected because there is something very powerful and important happening.
Look at the diagrams again.
Compare and contrast the blue-boxed lower and upper groups.
Do you see this amazing thing yet?
The upper group of C matches exactly the lower group of G.
The upper group of G matches exactly the lower group of D.
Holy macaroni!
That’s amazing.

15 Likes
It is time to view all major scales with the eight notes of the octaves grouped into the lower and upper groups of four. The scales are organised in alphabetical order from A major down to Ab major. The arrangement is deliberate. Major sales with flat notes are listed on the left side. Major scales with sharp notes are on the right. C major contains neither and is centred.
Note: the enharmonic equivalents F# and Gb are included and are shown side-by-side.
Split Major Scales in all 12 Keys
9 Likes
QUIZ TIME
We have just seen that the upper group of C makes a pair with the lower group of G and that the upper group of G makes a pair with the lower group of D.
Okay, it’s time for a little quiz of Match the Pairs.
Get your thinking hats on. Pour a drink. Have pen and paper at hand. The challenge is as follows.
For all twelve listed major scales, look at their upper groups and find a major scale whose lower group is a match. Also, look at their lower groups and find a major scale whose upper group is a match.
The matches should be:
Upper < — > Lower
and
Lower < — > Upper
Create an answer sheet like this:
or download and print from this link.
The matching pairs (seen above) between the major scales of C, G and D respectively have already been added.
Good luck.
9 Likes
Note -
Beware when seeking answers for the Gb / F# combination. I have placed these side-by-side, reading from left-to-right, as they are enharmonic equivalents.
You are only seeking one matching pair for the Gb (it will contain flats) and one matching pair for the F# (it will contain sharps).
Find a major scale that has a lower cluster of four that matches with the upper cluster of Gb.
Find a major scale with an upper cluster of four that matches the lower cluster of F#.
Thank you to @stitch for alerting me to the potential for confusion and giving feedback on this.
6 Likes
Anyone who has read to this point and taken the quiz - thank you, thank you, thank you. Of course, you do want to know the correct matching pairs so here are the answers:
Click here to read the hidden answers ...
How did you do?

9 Likes
Hopefully you have been finding matching pairs and completed the quiz.

If so, muchas gracias and I hope you found it beneficial.
If not, well, no problem … it’s not a strict prerequisite. Just a bit of a fun challenge and optional preparation to give a greater insight before progressing. It is okay to move on without it.
But before moving on, let us see the matching pairs - all matched up. Right in front of our eyes.
These are presented in alphabetical order to match with questions 1-12 on the quiz sheet.
6 Likes
ALERT - answers to the quiz below.
If you do not wish to see them yet please do not read on just yet.

Q1 - A major pairs: D ← lower – A – upper → E
Q2 - Bb major pairs : Eb ← lower – Bb – upper → F
Q3 - B major pairs : E ← lower – B – upper → F#
Q4 - C major pairs : F ← lower – C – upper → G
Q5 - Db major pairs : Gb ← lower – Db – upper → Ab
Q6 - D major pairs : G ← lower – D – upper → A
Q7 - Eb major pairs : Ab ← lower – Eb – upper → Bb
Q8 - E major pairs : A ← lower – E – upper → B
Q9 - F major pairs : Bb ← lower – F – upper → C
Q10 (a) - Gb major pairs : N/A ← lower – Gb – upper → Db
Q10 (b) - F# major pairs : B ← lower – F# – upper → N/A
Q11 - G major pairs : C ← lower – G – upper → D
Q12 - Ab major pairs : Db ← lower – Ab – upper → Eb
4 Likes
It is time to move on from the basics of pattern spotting, seeking how the note clusters within keys overlap. Time to move on and begin ‘circling’ - albeit circling in small steps.
The first step towards that is to shift the thinking away from having the scales arranged in alphabetical order. It offers little help beyond this point. It has served its purpose as an organisational hierarchy. And even then, it was not entirely essential, more to do with familiarity and ease. What we need instead is a new ordering of scales - not determined by the alphabetical names but by patterns of overlapping notes we have just discovered. This organising principle will also place together those scales that are the most alike, as will be seen.
4 Likes
To begin, we will remove A major from first in the list and bring C major to the first position.
The reasoning is simply that the C major scale contains no accidentals.
It is the white keys only when played on a keyboard.
It is the base sauce when preparing a savoury dish.
It is the flat lands before the mountains come into view.
It is the blank canvas upon which all colours and detail can be painted
If being harsh we could say it is the most bland.
Whatever the description, C major will be used as a ‘starting point’, an initial ‘reference scale’ as we proceed.
Using what we have just discovered with the four-note clusters, the process here is to think, which scales are the most similar to it? Which scales have an overlap with C major at the upper and lower ends?
4 Likes
From the diagram above we can see that G major and F major both overlap C major, one at each end respectively.
These three will be placed adjacent to each other with C in the middle.
Next, we will consider which scales will follow on in succession from aligning overlapping four-note clusters. Which scale follows on from the G and from the F major scales respectively? Which scales follow on after that? And so on.
What we are creating here can be viewed as two branches growing from the same source - our C major scale reference point.
We will look at each separately to begin.
4 Likes
First, we will follow the branches as they grow from the upper clusters - reading the patterns from left-to-right for the moment.
Overlapping clusters from C to F#
By following the overlaps left-to-right / top-to-bottom we create a stepped path of major scales that reads:
C → G → D → A → E → B → F#
4 Likes
Second, we follow the branches as they grow from the lower clusters, reading the patterns from right to left.
Overlapping clusters from C to Gb
If we now reverse start point and direction, and think of following the overlaps left-to-right / bottom-to-top we create a stepped path of major scales that reads:
Gb → Db → Ab → Eb → Bb → F → C
4 Likes